The redesigned Blogccasion is live
I started to blog way back in 2005, and while I was skeptical whether it would work out and was worth my time, I just tried it and danced 💃 and wrote like no one was watching (which definitely was the case for a while). Many of these early posts are slightly embarrassing from today's point of view, but nevertheless I decided to keep them around, since they are a part of me. Remember, this was before social networks became a thing. Actually, social networks almost killed my blogging, in both 2016 and 2017 respectively I only wrote one post, but plenty of tweets and Facebook posts. Here's a screenshot of the old blog:
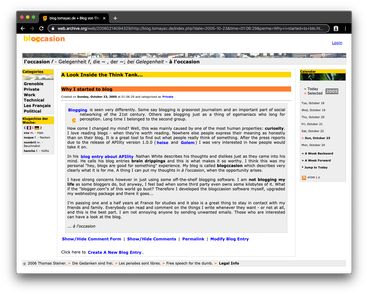
One of the reasons why I blogged less was also my hand-rolled stack that the blog was built upon: A classic LAMP stack, consisting of Linux, Apache, MySQL, and handwritten PHP 5. Since I had (and still have) no clue of MySQL character encoding configuration, I couldn't store emoji 🤔 in my database, but hey ¯\_(ツ)_/¯. The switch to HTTPS then killed my login system (that before on HTTP anyone could have sniffed, did I mention I was clueless?). In the end I had to log into phpMyAdmin to enter a new blog post into the database by hand. It was clearly time for a change.
Luckily this was the time when static site builders became more and more popular. I had heard good things of Zach Leatherman's Eleventy, so I went for it. It was super helpful to have the eleventy-base-blog repository that shows how to get started with Eleventy. I took extra care to make sure all my old URLs still worked, and learned more than I wanted about .htaccess files and .htaccess rewrite maps, since we all know that cool URIs don't change. There I was with a modern stack, and a 2005 design.
Now, I've finally also updated the design, and, while I'm not a designer, I still quite like it. Obviously it supports prefers-color-scheme, aka. Dark Mode and also uses the <dark-mode-toggle> custom element, but I've also decided to go for a responsive "holy grail" layout that is based on CSS Grid.
Here're the resources that helped me build the new Blogccasion:
- The circuit board SVG background is from Steve Schoger's site Hero Patterns.
- The core of my CSS Grid code is from Alligator's article CSS Grid: Holy Grail Layout. I learned about the particularities of Grid's minimum size of an
frunit, which isautoand which caused a Grid blowout described in Chris Coyier's aptly named article Preventing a Grid Blowout. - The Webmentions integration is from Sia Karamalego's article An In-Depth Tutorial of Webmentions + Eleventy.
- Some of the typography is inspired by Matej Latin's article 5 Keys to Accessible Web Typography and the Tufte CSS code.
- The SVG icons are from the SuperTinyIcons project.
- Some of the CSS is based on Mozilla's CSS Remedy project.
- Last not least, the Valid HTML5 badge is inspired by Bradley Taunt's article Using HTML Validator Badges Again.
- The Synthwave '84 code theme for Visual Studio Code originally is from Robb Owen. I'm using the port for PrismJS by Marc Backes.
🙏 Thanks everyone for letting me stand on your shoulders!
There're still some rough edges, so if you encounter a problem, please report an issue. It's well-known that there're a lot of encoding errors in the older posts. At some point I broke my database in an attempt to convert it to UTF-8 🤦♂️… If you care, you can also propose an edit straightaway, the edit this page on GitHub link is 👇 at the bottom of each post. Thanks, and welcome to the new Blogccasion.
